Snowflake Simulation
3D physically-based snowflake simulation at the mesoscopic scale, implemented in Houdini using VEX.
Overview
In Houdini, I implemented a physically-based model to simulate the formuation of snowflakes, following the paper “Modeling Snow Crystal Growth III: Three-Dimensional Snowfakes” by Janko Gravner and David Griffeath. The model works on a mesoscopic scale, or approximately the micron level. This works well for capturing the overall growth patterns of ice crystals without getting bogged down with tracking every water molecule.
They focus on three key factors for snowflake growth: water vapor diffusion, anisotropic attachment of water molecules, and a semi-liquid boudnary layer on the surface of the ice crystal. By adjusting these parameters, this model can produce a wide variety of realistic snowflakes.
The algorithm below was implemented in a SOP solver using VEX.
Algorithm
The paper’s model assumes the basic building cell of an ice crystal is a hexagonal prism, with a height of 1 and a hexagonal base length of 1/√3. At each site that an ice crystal can attach to \(x\) and time step \(t\), we keep track of two quantities: the boundary mass \(b_t(x)\) and diffusion mass \(d_t(x)\).
Diffusive mass represents water vapor in the air, and boundary mass reprsents the thin semi-liquid layer at the snowflake’s surface that vapor can condense into before freezing into solid ice. Together, they determine whether a cell will attach to the snow crystal (freezing).
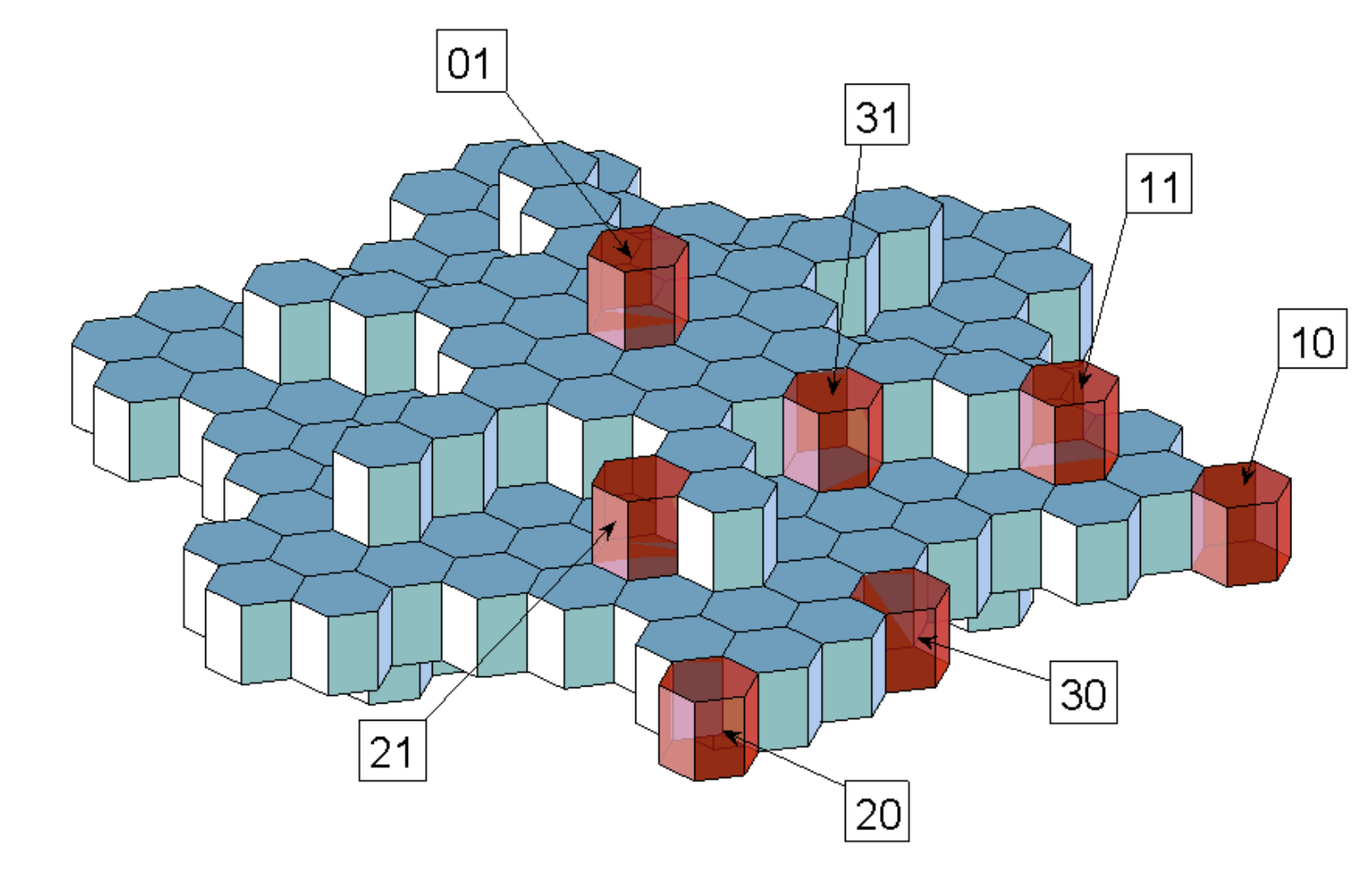
The algorithm is as follows:
1. Diffusion Calculation
Calculate the diffusion by averaging the vapor diffusion mass among each cell’s 6 horizontal neighbors and 2 vertical ones.
2. Freezing
Using the horizontal and vertical neighbors, calculate the boundary mass at each time step. If the boundary mass of a cell is greater than that of its neighbors, it freezes and we can attach the cell to the ice crystal.
Additionally, we can attach a cell to the crystal if all its horizontal and vertical neighbors are attached, in order to avoid holes and make the surface of the crystal smoother.
3. Metling
When melting, part of the boundary mass becomes diffusive mass.
Houdini Modeling
The initial state is a prism of hexagonal cells in a finite lattice:

Cells belong to one of three groups: snowflake (part of the crystal), boundary (at the semi-liquid surface layer), or vapor (diffuse). A SOP solver tracks the state of each cell and calculates the diffusion, freezing, and melting steps in VEX and applies updates at each iteration.
Simulation Results
Using parameters provided by the paper, I was able to generate the following result!

Notice the realistic snowflake features such as the branched dendrites and ridged plates. This model was a more physics-based approach to snowflake simulation versus a more art-directable one, so while it may not be very useful for a film’s snow VFX, it was a fun way for me to learn about VEX and solvers in Houdini.